An introductory example

This file contains an introductory example to define and traverse a simple quadrilateral mesh. The code for this example can be found in axom/src/axom/slam/examples/UserDocs.cpp.

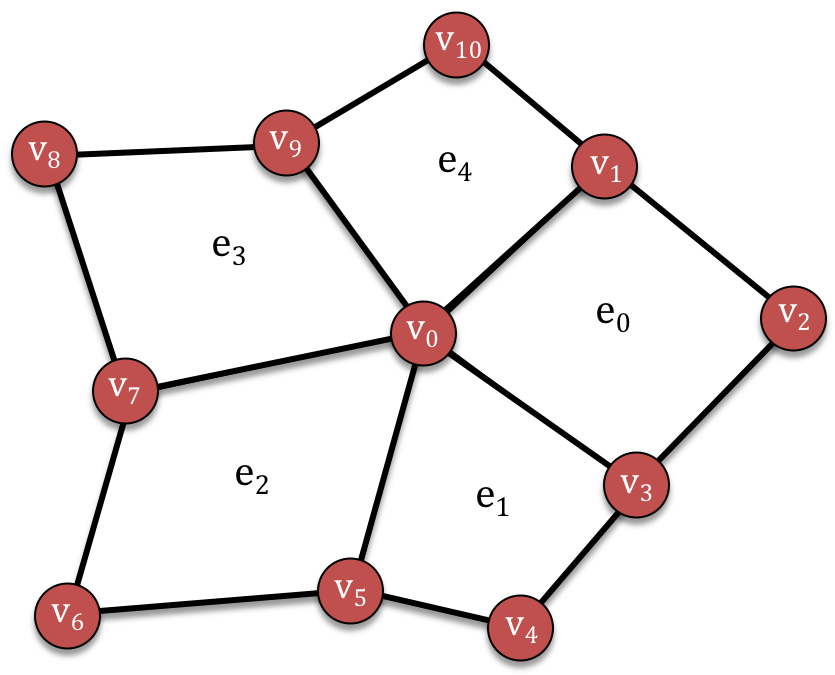
Fig. 32 An unstructured mesh with eleven vertices (red circles) and five elements (quadrilaterals bounded by black lines)

We first import the unified Slam header, which includes all necessary files for working with slam:

#include "axom/slam.hpp"

Note

All code in slam is in the axom::slam namespace. For convenience, we add the following namespace declaration to our example to allow us to directly use the slam namespace:

namespace slam = axom::slam;

Type aliases and variables

We begin by defining some type aliases for the Sets, Relations and Maps in our mesh. These type aliases would typically be found in a configuration file or in class header files.

We use the following types throughout this example:

  using ArrayIndir = slam::policies::CArrayIndirection<PosType, ElemType>;

Sets

Our mesh is defined in terms of two sets: Vertices and Elements, whose entities are referenced by integer-valued indices. Since both sets use a contiguous range of indices starting from 0, we use slam::PositionSet to represent them.

We define the following type aliases:

  using PosType = slam::DefaultPositionType;
  using ElemType = slam::DefaultElementType;
  using VertSet = slam::PositionSet<PosType, ElemType>;
  using ElemSet = slam::PositionSet<PosType, ElemType>;

and declare them as:

  VertSet verts;  // The set of vertices in the mesh
  ElemSet elems;  // The set of elements in the mesh

For other available set types, see Set.

Relations

We also have relations describing the incidences between the mesh vertices and elements.

The element-to-vertex boundary relation encodes the indices of the vertices in the boundary of each element. Since this is a quad mesh and there are always four vertices in the boundary of a quadrilateral, we use a ConstantCardinality policy with a CompileTimeStride set to 4 for this StaticRelation.

  // Type aliases for element-to-vertex boundary relation
  enum
  {
    VertsPerElem = 4
  };
  using CTStride = slam::policies::CompileTimeStride<PosType, VertsPerElem>;
  using ConstCard = slam::policies::ConstantCardinality<PosType, CTStride>;
  using ElemToVertRelation =
    slam::StaticRelation<PosType, ElemType, ConstCard, ArrayIndir, ElemSet, VertSet>;

The vertex-to-element coboundary relation encodes the indices of all elements incident in each of the vertices. Since the cardinality of this relation changes for different vertices, we use a VariableCardinality policy for this StaticRelation.

  // Type aliases for vertex-to-element coboundary relation
  using VarCard = slam::policies::VariableCardinality<PosType, ArrayIndir>;
  using VertToElemRelation =
    slam::StaticRelation<PosType, ElemType, VarCard, ArrayIndir, VertSet, ElemSet>;

We declare them as:

  ElemToVertRelation bdry;    // Boundary relation from elements to vertices
  VertToElemRelation cobdry;  // Coboundary relation from vertices to elements

For other available set types, see Relation.

Maps

Finally, we have some maps that attach data to our sets.

The following defines a type alias for the positions of the mesh vertices. It is templated on a point type (Point2) that handles simple operations on 2D points.

  using BaseSet = slam::Set<PosType, ElemType>;
  using ScalarMap = slam::Map<Point2, BaseSet>;
  using PointMap = slam::Map<Point2, BaseSet>;
  using VertPositions = PointMap;

It is declared as:

  VertPositions position;  // vertex position

Constructing the mesh

This example uses a very simple fixed mesh, which is assumed to not change after it has been initialized.

Sets

The sets are created using a constructor that takes the number of elements.

    verts = VertSet(11);  // Construct vertex set with 11 vertices
    elems = ElemSet(5);   // Construct the element set with 5 elements

The values of the vertex indices range from 0 to verts.size()-1 (and similarly for elems).

Note

All sets, relations and maps in Slam have internal validity checks using the isValid() function:

    SLIC_ASSERT_MSG(verts.isValid(), "Vertex set is not valid.");
    SLIC_ASSERT_MSG(elems.isValid(), "Elment set is not valid.");

Relations

The relations are constructed by binding their associated sets and arrays of data to the relation instance. In this example, we use an internal helper class RelationBuilder.

We construct the boundary relation by attaching its two sets (elems for its fromSet and verts for its toSet) and an array of indices for the relation’s data.

      // construct boundary relation from elements to vertices
      using RelationBuilder = ElemToVertRelation::RelationBuilder;
      bdry = RelationBuilder().fromSet(&elems).toSet(&verts).indices(
        RelationBuilder::IndicesSetBuilder()
          .size(static_cast<int>(evInds.size()))
          .data(evInds.data()));

The Coboundary relation requires an additional array of offsets (begins) to indicate the starting index in the relation for each vertex:

      // construct coboundary relation from vertices to elements
      using RelationBuilder = VertToElemRelation::RelationBuilder;
      cobdry = RelationBuilder()
                 .fromSet(&verts)
                 .toSet(&elems)
                 .begins(RelationBuilder::BeginsSetBuilder()
                           .size(verts.size())
                           .data(veBegins.data()))
                 .indices(RelationBuilder::IndicesSetBuilder()
                            .size(static_cast<int>(veInds.size()))
                            .data(veInds.data()));

Since these are static relations, we used data that was constructed elsewhere. Note that these relations are lightweight wrappers over the underlying data – no data is copied. To iteratively build the relations, we would use the DynamicConstantRelation and DynamicVariableRelation classes.

See Simplifying mesh setup for more details about Slam’s Builder classes for sets, relations and maps.

Maps

We define the positions of the mesh vertices as a Map on the verts set. For this example, we set the first vertex to lie at the origin, and the remaining vertices line within an annulus around the unit circle.

    // construct the position map on the vertices
    position = VertPositions(&verts);

    // first vertex is at origin
    position[0] = Point2(0., 0.);

    // remaining vertices lie within annulus around unit disk
    // in cw order, starting at angleOffset
    constexpr double rInner = 0.8;
    constexpr double rOuter = 1.2;
    constexpr double angleOffset = 0.75;
    const double N = verts.size() - 1;

    for(int i = 1; i < verts.size(); ++i)
    {
      const double angle = -(i - 1) / N * 2 * M_PI + angleOffset;
      const double mag = axom::utilities::random_real(rInner, rOuter);

      position[i] = Point2(mag * std::cos(angle), mag * std::sin(angle));
    }

Traversing the mesh

Now that we’ve constructed the mesh, we can start traversing the mesh connectivity and attaching more fields.

Computing a derived field

Our first traversal loops through the vertices and computes a derived field on the position map. For each vertex, we compute its distance to the origin.

    // Create a Map of scalars over the vertices
    ScalarMap distances(&verts);

    for(int i = 0; i < distances.size(); ++i)  // <-- Map::size()
    {
      auto vID = verts[i];               // <-- Set::operator[]
      const Point2& pt = position[vID];  // <-- Map::operator[]

      distances[i] = std::sqrt(pt[0] * pt[0]  // <-- Map::operator[]
                               + pt[1] * pt[1]);
    }

Computing element centroids

Our next example uses element-to-vertex boundary relation to compute the centroids of each element as the average of its vertex positions.

    // Create a Map of Point2 over the mesh elements
    using ElemCentroidMap = PointMap;
    ElemCentroidMap centroid = ElemCentroidMap(&elems);

    // for each element...
    for(int eID = 0; eID < elems.size(); ++eID)  // <-- Set::size()
    {
      Point2 ctr;

      auto elVerts = bdry[eID];  // <-- Relation::operator[]

      // find average position of incident vertices
      for(int i = 0; i < elVerts.size(); ++i)  // <-- Set::size()
      {
        auto vID = elVerts[i];  // <-- Set::operator[]
        ctr += position[vID];   // <-- Map::operator[]
      }
      ctr /= elVerts.size();  // <-- Set::size())
      centroid[eID] = ctr;    // <-- Map::operator[]
    }

Perhaps the most interesting line here is when we call the relation’s subscript operator (bdry[eID]). This function takes an element index (eID) and returns the set of vertices that are incident in this element. As such, we can use all functions in the Set API on this return type, e.g. size() and the subscript operator.

Outputting mesh to disk

As a final example, we highlight several different ways to iterate through the mesh’s Sets, Relations and Maps as we output the mesh to disk (in the vtk format).

This is a longer example, but the callouts (left-aligned comments of the form // <-- message ) point to different iteration patterns.

    std::ofstream meshfile;
    meshfile.open("quadMesh.vtk");
    std::ostream_iterator<PosType> out_it(meshfile, " ");

    // write header
    meshfile << "# vtk DataFile Version 3.0\n"
             << "vtk output\n"
             << "ASCII\n"
             << "DATASET UNSTRUCTURED_GRID\n\n"
             << "POINTS " << verts.size() << " double\n";

    // write positions
    for(auto pos : position)  // <-- Uses range-based for on position map
    {
      meshfile << pos[0] << " " << pos[1] << " 0\n";
    }

    // write elem-to-vert boundary relation
    meshfile << "\nCELLS " << elems.size() << " " << 5 * elems.size();
    for(auto e : elems)  // <-- uses range-based for on element set
    {
      meshfile << "\n4 ";
      std::copy(bdry.begin(e),  // <-- uses relation's iterators
                bdry.end(e),
                out_it);
    }

    // write element types ( 9 == VKT_QUAD )
    meshfile << "\n\nCELL_TYPES " << elems.size() << "\n";
    for(int i = 0; i < elems.size(); ++i)
    {
      meshfile << "9 ";
    }

    // write element ids
    meshfile << "\n\nCELL_DATA " << elems.size() << "\nSCALARS cellIds int 1"
             << "\nLOOKUP_TABLE default \n";
    for(int i = 0; i < elems.size(); ++i)
    {
      meshfile << elems[i] << " ";  // <-- uses size() and operator[] on set
    }

    // write vertex ids
    meshfile << "\n\nPOINT_DATA " << verts.size() << "\nSCALARS vertIds int 1"
             << "\nLOOKUP_TABLE default \n";
    for(int i = 0; i < verts.size(); ++i)
    {
      meshfile << verts[i] << " ";
    }
    meshfile << "\n";