Orientation¶
Axom contains two overloads of orientation(). The 3D case tests a point against
a triangle and reports which side it lies on; the 2D case tests a point against a
line segment. Here is an example of the 3D point-triangle orientation test.
#include "axom/primal/operators/orientation.hpp"
// A triangle
TriangleType tri(PointType {1.2, 0, 0},
PointType {0, 1.8, 0},
PointType {0, 0, 1.4});
// Three points:
// one on the triangle's positive side,
PointType pos = PointType {0.45, 1.5, 1};
// one coplanar to the triangle, the centroid,
PointType cpl =
PointType::lerp(PointType::lerp(tri[0], tri[1], 0.5), tri[2], 1. / 3.);
// and one on the negative side
PointType neg = PointType {0, 0, 0.7};
// Test orientation
if(orientation(pos, tri) == primal::ON_POSITIVE_SIDE &&
orientation(cpl, tri) == primal::ON_BOUNDARY &&
orientation(neg, tri) == primal::ON_NEGATIVE_SIDE)
{
std::cout << "As expected, point pos is on the positive side," << std::endl
<< " point cpl is on the boundary (on the triangle),"
<< std::endl
<< " and point neg is on the negative side." << std::endl;
}
else
{
std::cout << "Someone wrote this wrong." << std::endl;
}
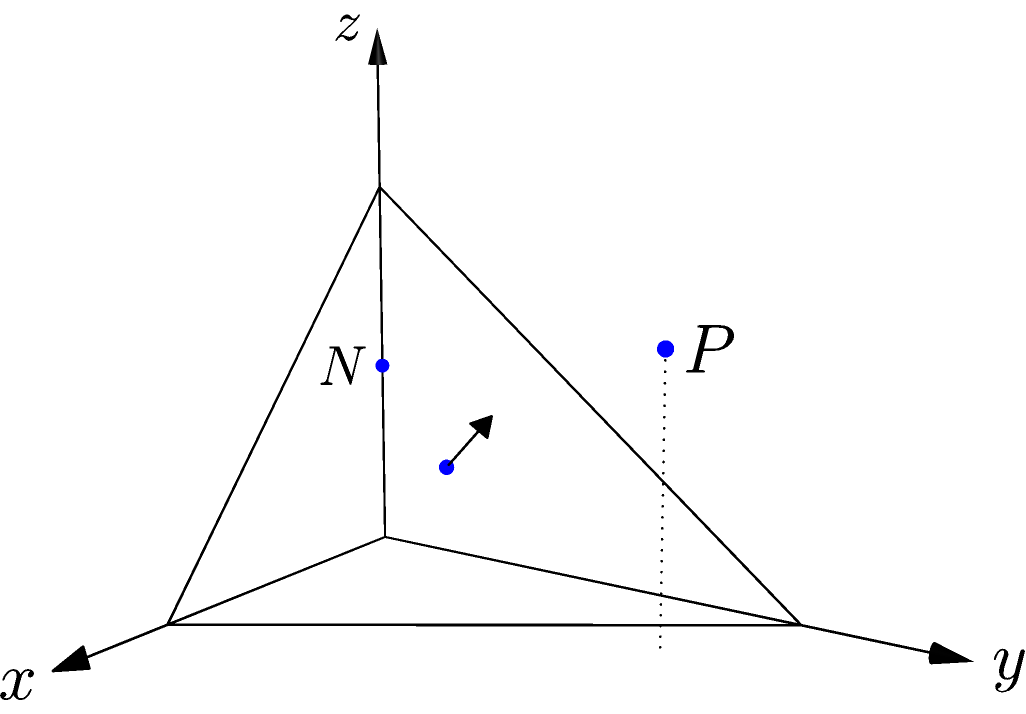
The triangle is shown with its normal vector pointing out of its centroid. The triangle’s plane divides space into a positive half-space, pointed into by the triangle’s normal vector, and the opposing negative half-space. The test point on the \(z\) axis, labelled \(N\), is on the negative side of the triangle. The centroid lies in the triangle, on the boundary between the two half-spaces. The remaining test point, labelled \(P\), is on the triangle’s positive side.