Intersection

The intersection test is provided by intersect(). It takes two primitives and returns a boolean indicating if the primitives intersect. Some overloads return the point of intersection in an output argument. The overloads for intersect() are summarized in the table below.

Arg 1	Arg 2	Additional arguments and notes
Triangle	Triangle	include boundaries [1] (default false)
Ray	Segment	return intersection point. 2D only.
Segment	BoundingBox	return intersection point
Ray	BoundingBox	return intersection point
BoundingBox	BoundingBox
Sphere	Sphere	specify tolerance
Triangle	BoundingBox
Triangle	Ray	return parameterized intersection point (on Ray), return barycentric intersection point (on Triangle)
Triangle	Segment	return parameterized intersection point (on Segment), return barycentric intersection point (on Triangle)
OrientedBoundingBox	OrientedBoundingBox	specify tolerance

[1]

By default, the triangle intersection algorithm considers only the triangles’ interiors, so that non-coplanar triangles that share two vertices are not reported as intersecting. The caller to intersect() can specify an optional argument to include triangle boundaries in the intersection test.

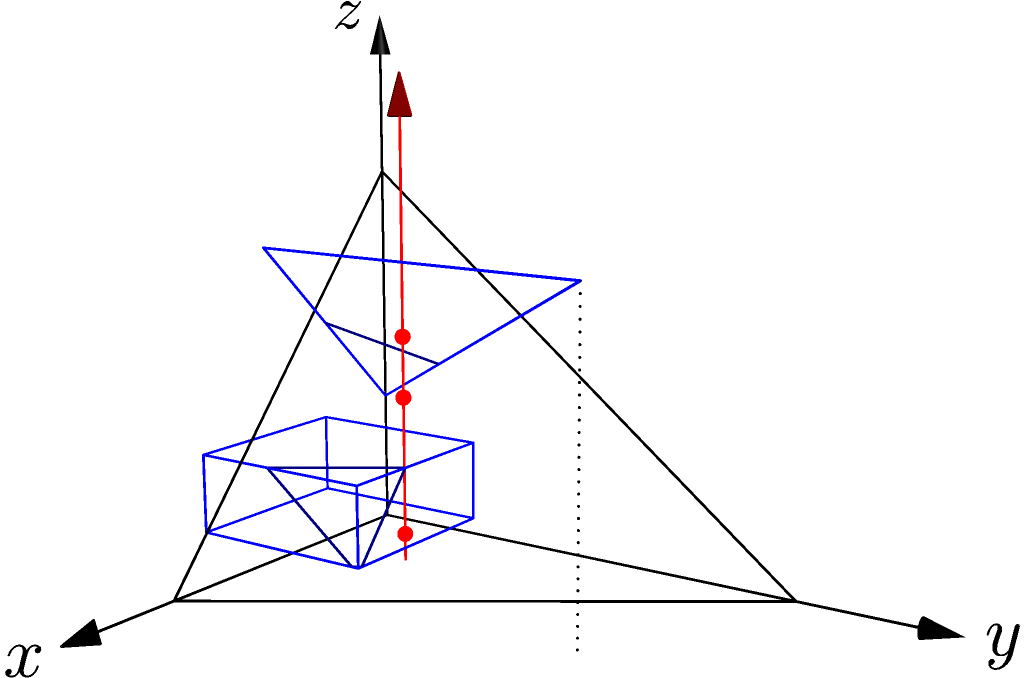
The example below tests for intersection between two triangles, a ray, and a BoundingBox.

#include "axom/primal/operators/intersect.hpp"

  // Two triangles
  TriangleType tri1(PointType {1.2, 0, 0},
                    PointType {0, 1.8, 0},
                    PointType {0, 0, 1.4});

  TriangleType tri2(PointType {0, 0, 0.5},
                    PointType {0.8, 0.1, 1.2},
                    PointType {0.8, 1.4, 1.2});

  // tri1 and tri2 should intersect
  if(intersect(tri1, tri2))
  {
    std::cout << "Triangles intersect as expected." << std::endl;
  }
  else
  {
    std::cout << "There's an error somewhere..." << std::endl;
  }

  // A vertical ray constructed from origin and point
  RayType ray(SegmentType(PointType {0.4, 0.4, 0}, PointType {0.4, 0.4, 1}));

  // t will hold the intersection point between ray and tri1,
  // as parameterized along ray.
  double rt1t = 0;
  // rt1b will hold the intersection point barycentric coordinates,
  // and rt1p will hold the physical coordinates.
  PointType rt1b, rt1p;

  // The ray should intersect tri1 and tri2.
  if(intersect(tri1, ray, rt1t, rt1b) && intersect(tri2, ray))
  {
    // Retrieve the physical coordinates from barycentric coordinates
    rt1p = tri1.baryToPhysical(rt1b);
    // Retrieve the physical coordinates from ray parameter
    PointType rt1p2 = ray.at(rt1t);
    std::cout << "Ray intersects tri1 as expected.  Parameter t: " << rt1t
              << std::endl
              << "  Intersection point along ray: " << rt1p2 << std::endl
              << "  Intersect barycentric coordinates: " << rt1b << std::endl
              << "  Intersect physical coordinates: " << rt1p << std::endl
              << "Ray also intersects tri2 as expected." << std::endl;
  }
  else
  {
    std::cout << "There's an error somewhere..." << std::endl;
  }

  // A bounding box
  BoundingBoxType bbox(PointType {0.1, -0.23, 0.1}, PointType {0.8, 0.5, 0.4});

  // The bounding box should intersect tri1 and ray but not tr2.
  PointType bbtr1;
  if(intersect(ray, bbox, bbtr1) && intersect(tri1, bbox) &&
     !intersect(tri2, bbox))
  {
    std::cout << "As hoped, bounding box intersects tri1 at " << bbtr1
              << " and ray, but not tri2." << std::endl;
  }
  else
  {
    std::cout << "There is at least one error somewhere..." << std::endl;
  }

In the diagram, the point where the ray enters the bounding box is shown as the intersection point (not the exit point or some point inside the box). This is because if a ray intersects a bounding box at more than one point, the first intersection point along the ray (the intersection closest to the ray’s origin) is reported as the intersection. If a ray originates inside a bounding box, the ray’s origin will be reported as the point of intersection.