Mesh Representation¶
Irrespective of the mesh type, a mesh essentially provides a data structure that enables efficient storage, management and access of:
Mesh Geometry information (i.e., nodal coordinates),
Mesh Topology information (i.e., cell-to-node connectivity, etc.), and
Field Data stored on a mesh
The underlying, concrete representation of the Geometry and Topology of a mesh is the key distinguishing characteristic used to classify a mesh into the different Mesh Types. As a prerequisite to the proceeding discussion on the taxonomy of the various Mesh Types, this section provides a high level description of the key constituents of the Mesh Representation. Namely, the Topology, Geometry and Field Data comprising a mesh.
Topology¶
The topology of a mesh, \(\mathcal{M}(\Omega) \in \mathbb{R}^d\), is defined by the collection of topological entities, e.g. the Cells, Faces and Nodes, comprising the mesh and the associated adjacency information that encodes the topological connections between them, broadly referred to as Connectivity information. Each topological entity in the mesh is identified by a unique index, as depicted in the sample Unstructured Mesh shown in Fig. 4. This provides a convenient way to traverse and refer to individual entities in the mesh.
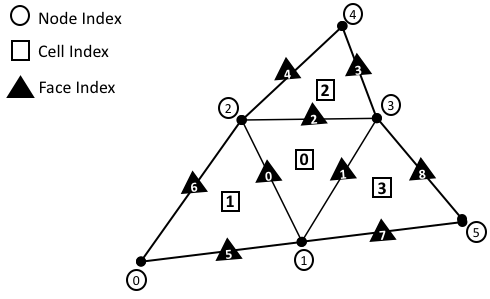
Fig. 4 Sample unstructured mesh. Each node, cell and face on the mesh has a unique index.¶
In Mint, the three fundamental topological entities comprising a mesh are (1) Cells, (2) Faces, and (3) Nodes.
Note
The current implementation does not provide first class support for edges and associated edge data in 3D. However, this is a feature we are planning to support in future versions of Mint.
Cells¶
A cell, \(\mathcal{C}_i\), is given by an ordered list of Nodes, \(\mathcal{C}_i=\{n_0,n_1,...n_k\}\), where each entry, \(n_j \in \mathcal{C}_i\), corresponds to a unique node index in the mesh. The order of Nodes defining a cell is determined according to a prescribed local numbering convention for a particular cell type. See Fig. 15 and Fig. 16. All Mint Cell Types follow the CGNS Numbering Conventions.
Faces¶
Similarly, a face, \(\mathcal{F}_i\), is defined by an ordered list of Nodes, \(\mathcal{F}_i=\{n_0,n_1,...,n_k\}\). Faces are essentially Cells whose topological dimension is one less than the dimension of the Cells they are bound to. See Fig. 5. Consequently, the constituent faces of a 3D cell are 2D topological entities, such as triangles or quads, depending on the cell type. The faces of a 2D cell are 1D topological entities, i.e. segments. Last, the faces of a 1D cell are 0D topological entities, i.e. Nodes.
Note
In 1D the Faces of a cell are equivalent to the constituent mesh Nodes, hence, Mint does not explicitly support Faces in 1D.
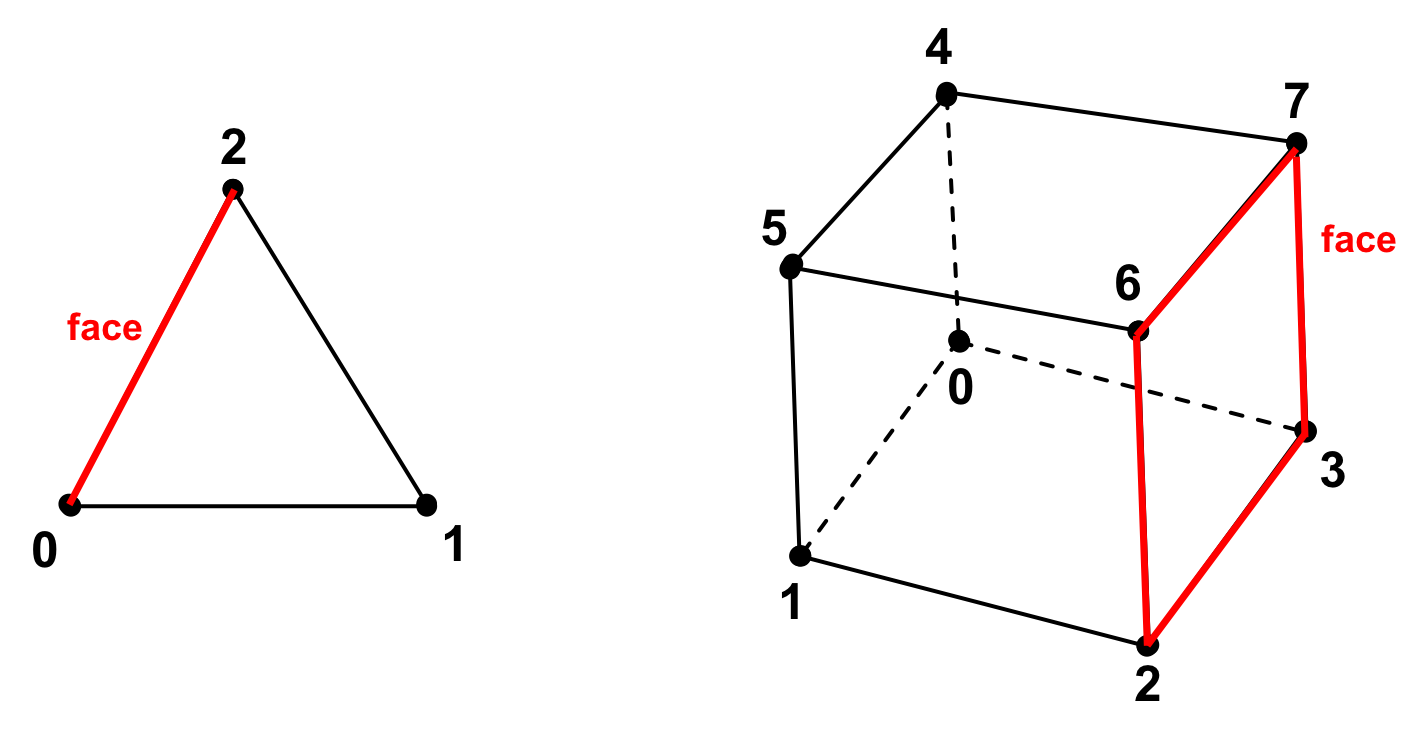
Fig. 5 Constituent faces of a cell in 2D and 3D respectively. the constituent faces of a 3D cell are 2D topological entities, such as triangles or quads, depending on the cell type. The faces of a 2D cell are 1D topological entities, i.e. segments.¶
Face Types
A mesh face can be bound to either one or two Cells:
Faces bound to two Cells, within the same domain, are called internal faces.
Faces bound to two Cells, across different domains (or partitions), are called internal boundary faces. Internal boundary faces define the communication boundaries where ghost data is exchanged between domains.
Faces bound to a single cell are called external boundary faces. External boundary faces (and/or their consistuent nodes) are typically associated with a boundary condition.
Note
By convention, \(\mathcal{C}_1\) is set to \(-1\) for external boundary faces, which are bound to a single cell.
Nodes¶
The Nodes are zero dimensional topological entities and hence, are the lowest dimensional constituent entities of a mesh. The Nodes are associated with the spatial coordinates of the mesh and are used in defining the topology of the higher dimensional topological entities comprising the mesh, such as the Cells, Faces, etc., as discussed earlier. In a sense, the Nodes provide the means to link the Topology of the mesh to its constituent Geometry and thereby instantiate the mesh in physical space.
Definition
A mesh node, \(\mathcal{n_i}\), is associated with a point, \(p_i \in \mathbb{R}^d\) and provides the means to:
Notably, the nodes of a mesh may be more than just the vertices of the mesh. As discussed in the Preliminary Concepts section, a mesh is a discretization of a PDE. Recall, the primary purpose of the mesh is to define the discrete locations, in both space and time, at which the unknown variables or degrees of freedom of the governing PDE are evaluated. Depending on the numerical scheme employed and the Cell Types used, additional mesh Nodes may be located on the constituent cell faces, edges and in the cell interior. For example, in the Finite Element Method (FEM), the nodes for the linear Lagrange Finite Elements, see Fig. 15, are located at the cell vertices. However, for quadratic Cell Types, see Fig. 16, the Lagrange \(P^2\) finite element, for the quadrilateral and hexahedron (in 3D) cells, includes as Nodes, the cell, face and edge (in 3D) centroids in addition to the cell vertices. Other higher order finite elements may involve additional nodes for each edge and face as well as in the interior of the cell.
Connectivity¶
The topological connections or adjecencies between the Cells, Faces and Nodes comprising the mesh, give rise to a hierarchical topological structure, depicted in Fig. 7, that is broadly referred to as Connectivity information. At the top level, a mesh consists of one or more Cells, which constitute the highest dimensional entity comprising the mesh. Each cell is bounded by zero or more Faces, each of which is bounded by one or more Nodes.
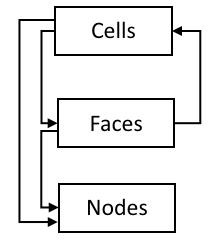
Fig. 7 Hierarchical topological structure illustrating the downward and upward topological connections of the constituent mesh entities supported in Mint.¶
The topological connections between the constituent entities of the mesh can be distinguished in (a) downward and (b) upward topological connections, as illustrated in Fig. 7.
The downward topological connections encode the connections from higher dimensional mesh entities to lower dimensional entities, such as cell-to-node, face-to-node or cell-to-face.
The upward topological connections, also called reverse connectivities, encode the connections from lower dimensional mesh entities to higher dimensional entities, such as face-to-cell.
Two key guiding considerations in the design and implementation of mesh data structures are storage and computational efficiency. In that respect, the various Mesh Types offer different advantages and tradeoffs. For example, the inherent regular topology of a Structured Mesh implicitly defines the Connectivity information. Consequently, the topological connections between mesh entities can be efficiently computed on-the-fly. However, for an Unstructured Mesh, the Connectivity information has to be extracted and stored explicitly so that it is readily available for computation.
An Unstructured Mesh representation that explicitly stores all \(0\) to \(d\) topological entities and associated downward and upward Connectivity information is said to be a full mesh representation. Otherwise, it is called a reduced mesh representation. In practice, it can be prohibitively expensive to store a full mesh representation. Consequently, most applications keep a reduced mesh representation.
The question that needs to be addressed at this point is what Connectivity information is generally required. The answer can vary depending on the application. The type of operations performed on the mesh impose the requirements for the Connectivity information needed. The minimum sufficient representation for an Unstructured Mesh is the cell-to-node Connectivity, since, all additional Connectivity information can be subsequently computed based on this information.
In an effort to balance both flexibility and simplicity, Mint, in its simplest form, employs the minumum sufficient Unstructured Mesh representation, consisting of the cell-to-node Connectivity. This allows applications to employ a fairly light-weight mesh representation when possible. However, for applications that demand additional Connectivity information, Mint provides methods to compute the needed additional information.
Warning
The present implementation of Mint provides first class support for cell-to-node, cell-to-face, face-to-cell and face-to-node Connectivity information for all the Mesh Types. Support for additional Connectivity information will be added in future versions based on demand by applications.
Geometry¶
The Geometry of a mesh is given by a set of Nodes. Let \(\mathcal{N}=\{n_0, n_1, n_2, ..., n_k\}\) be the finite set of nodes comprising a mesh, \(\mathcal{M}(\Omega) \in \mathbb{R}^d\), where \(d\) is the spatial dimension, \(d \in \{1,2,3\}\). Each node, \(n_i \in \mathcal{N}\), corresponds to a point, \(p_i \in \mathbb{R}^d\), whose spatial coordinates, i.e. an ordered tuple, define the physical location of the node in space, \(n_i \in \mathbb{R}^d\) . The Nodes link the Geometry of the mesh to its Topology. The Geometry and Topology of the mesh collectively define the physical shape, size and location of the mesh in space.
Field Data¶
The Field Data are used to define various physical quantities over the constituent mesh entities, i.e. the Cells, Faces and Nodes of the mesh. Each constituent mesh entity can be associated with zero or more fields, each of which may correspond to a scalar, vector or tensor quantity, such as temperature, velocity, pressure, etc. Essentially, the Field Data are used to define the solution to the unknown variables of the governing PDE that are evaluated on a given mesh, as well as, any other auxiliary variables or derived quantities that an application may need.
Warning
The present implementation of Mint supports Field Data defined on Cells, Faces and Nodes. Support for storing Field Data on edges will be added in future versions based on application demand.