Finite Elements
The Finite Element Method (FEM) is a widely used numerical technique, employed
for the solution of partial differential equations (PDEs), arising in
structural engineering analysis and more broadly in the field of
continuum mechanics.
However, due to their generality and mathematically sound foundation,
Finite Elements, are often employed in the implementation of other numerical
schemes and for various computational operators, e.g. interpolation,
integration, etc.
Mint provides basic support for Finite Elements that consists:
Lagrange Basis shape functions for commonly employed Cell Types
Corresponding Quadratures (under development)
Routines for forward/inverse Isoparametric Mapping, and
Infrastructure to facilitate adding shape functions for
new Cell Types, as well as, to Add a New Finite Element Basis.
This functionality is collectively exposed to the application through the
mint::FiniteElement class. Concrete examples illustrating the usage of the
mint::FiniteElement class within an application code are provided in the
Finite Elements tutorial section.
A Finite Element Basis consists of a family of shape functions
corresponding to different Cell Types. Mint currently supports
Lagrange isoparametric Finite Elements.
Lagrange Basis
The Lagrange basis consists of Cell Types whose shape functions are
formed from products of the one-dimensional Lagrange polynomial. This
section provides a summary of supported Lagrange Basis Cell Types,
their associated shape functions, and summarize the process to
Add a New Lagrange Element.
Note
The shape functions of all Lagrange Cells in Mint, follow the
CGNS Numbering Conventions and are defined within a reference coordinate
system, on the closed interval \(\hat{\xi} \in [0,1]\).
QUAD: Linear Quadrilateral
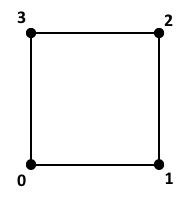
\begin{array}{r c l c l}
N_0 &=& (1 - \xi) &\times& (1 - \eta) \\
N_1 &=& \xi &\times& (1 - \eta) \\
N_2 &=& \xi &\times& \eta \\
N_3 &=& (1 - \xi) &\times& \eta \\
\end{array}
QUAD9: Quadratic Quadrilateral
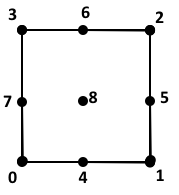
\begin{array}{r c l c l}
N_0 &=& (\xi-1)( 2\xi -1) &\times& (\eta-1)(2\eta-1) \\
N_1 &=& \xi(2\xi-1) &\times& (\eta-1)(2\eta-1) \\
N_2 &=& \xi(2\xi-1) &\times& \eta(2\eta-1) \\
N_3 &=& (\xi-1)( 2\xi -1) &\times& \eta(2\eta-1) \\
\\
N_4 &=& 4\xi(1-\xi) &\times& (\eta-1)(2\eta-1) \\
N_5 &=& \xi(2\xi-1) &\times& 4\eta(1-\eta) \\
N_6 &=& 4\xi(1-\xi) &\times& \eta(2\eta-1) \\
N_7 &=& (\xi-1)( 2\xi -1) &\times& 4\eta(1-\eta) \\
\\
N_8 &=& 4\xi(1-\xi) &\times& 4\eta(1-\eta) \\
\end{array}
TRIANGLE: Linear Triangle
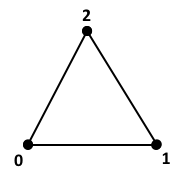
\begin{array}{r c l}
N_0 & = & 1 - \xi - \eta \\
N_1 & = & \xi \\
N_2 & = & \eta \\
\end{array}
HEX: Linear Hexahedron
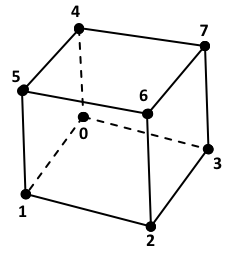
\begin{array}{r c l c l c l}
N_0 &=& (1-\xi) &\times& (1-\eta) &\times& (1-\zeta) \\
N_1 &=& \xi &\times& (1-\eta) &\times& (1-\zeta) \\
N_2 &=& \xi &\times& \eta &\times& (1-\zeta) \\
N_3 &=& (1-\xi) &\times& \eta &\times& (1-\zeta) \\
\\
N_4 &=& (1-\xi) &\times& (1-\eta) &\times& \zeta \\
N_5 &=& \xi &\times& (1-\eta) &\times& \zeta \\
N_6 &=& \xi &\times& \eta &\times& \zeta \\
N_7 &=& (1-\xi) &\times& \eta &\times& \zeta \\
\end{array}
HEX27: Quadratic Hexahedron
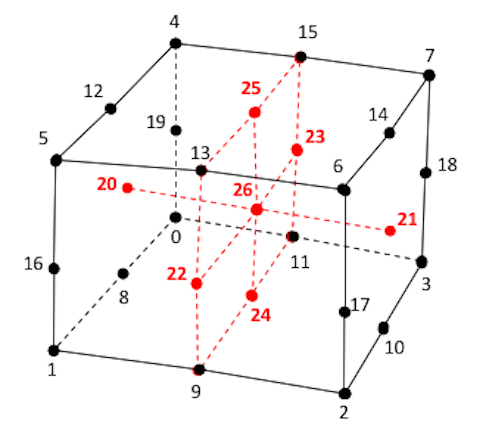
\begin{array}{r c l c l c l}
N_0 &=& (\xi-1)(2\xi-1) &\times& (\eta-1)(2\eta-1) &\times& (\zeta-1)(2\zeta-1) \\
N_1 &=& \xi(2\xi-1) &\times& (\eta-1)(2\eta-1) &\times& (\zeta-1)(2\zeta-1) \\
N_2 &=& \xi(2\xi-1) &\times& \eta(2\eta-1) &\times& (\zeta-1)(2\zeta-1) \\
N_3 &=& (\xi-1)(2\xi-1) &\times& \eta(2\eta-1) &\times& (\zeta-1)(2\zeta-1) \\
\\
N_4 &=& (\xi-1)(2\xi-1) &\times& (\eta-1)(2\eta-1) &\times& \zeta(2\zeta-1) \\
N_5 &=& \xi(2\xi-1) &\times& (\eta-1)(2\eta-1) &\times& \zeta(2\zeta-1) \\
N_6 &=& \xi(2\xi-1) &\times& \eta(2\eta-1) &\times& \zeta(2\zeta-1) \\
N_7 &=& (\xi-1)(2\xi-1) &\times& \eta(2\eta-1) &\times& \zeta(2\zeta-1) \\
\\
N_8 &=& 4\xi(1-\xi) &\times& (\eta-1)(2\eta-1) &\times& (\zeta-1)(2\zeta-1) \\
N_9 &=& \xi(2\xi-1) &\times& 4\eta(1-\eta) &\times& (\zeta-1)(2\zeta-1) \\
N_{10} &=& 4\xi(1-\xi) &\times& \eta(2\eta-1) &\times& (\zeta-1)(2\zeta-1) \\
N_{11} &=& (\xi-1)(2\xi-1) &\times& 4\eta(1-\eta) &\times& (\zeta-1)(2\zeta-1) \\
\\
N_{12} &=& 4\xi(1-\xi) &\times& (\eta-1)(2\eta-1) &\times& \zeta(2\zeta-1) \\
N_{13} &=& \xi(2\xi-1) &\times& 4\eta(1-\eta) &\times& \zeta(2\zeta-1) \\
N_{14} &=& 4\xi(1-\xi) &\times& \eta(2\eta-1) &\times& \zeta(2\zeta-1) \\
N_{15} &=& (\xi-1)(2\xi-1) &\times& 4\eta(1-\eta) &\times& \zeta(2\zeta-1) \\
\\
N_{16} &=& (\xi-1)(2\xi-1) &\times& (\eta-1)(2\eta-1) &\times& 4\zeta(1-\zeta) \\
N_{17} &=& \xi(2\xi-1) &\times& (\eta-1)(2\eta-1) &\times& 4\zeta(1-\zeta) \\
N_{18} &=& \xi(2\xi-1) &\times& \eta(2\eta-1) &\times& 4\zeta(1-\zeta) \\
N_{19} &=& (\xi-1)(2\xi-1) &\times& \eta(2\eta-1) &\times& 4\zeta(1-\zeta) \\
\\
N_{20} &=& (\xi-1)(2\xi-1) &\times& 4\eta(1-\eta) &\times& 4\zeta(1-\zeta) \\
N_{21} &=& \xi(2\xi-1) &\times& 4\eta(1-\eta) &\times& 4\zeta(1-\zeta) \\
N_{22} &=& 4\xi(1-\xi) &\times& (\eta-1)(2\eta-1) &\times& 4\zeta(1-\zeta) \\
N_{23} &=& 4\xi(1-\xi) &\times& \eta(2\eta-1) &\times& 4\zeta(1-\zeta) \\
N_{24} &=& 4\xi(1-\xi) &\times& 4\eta(1-\eta) &\times& (\zeta-1)(2\zeta-1) \\
N_{25} &=& 4\xi(1-\xi) &\times& 4\eta(1-\eta) &\times& \zeta(2\zeta-1) \\
\\
N_{26} &=& 4\xi(1-\xi) &\times& 4\eta(1-\eta) &\times& 4\zeta(1-\zeta) \\
\end{array}
PYRAMID: Linear Pyramid
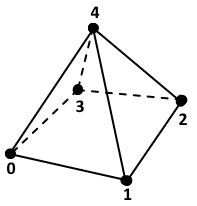
\begin{array}{r c l c l c l}
N_0 &=& (1-\xi) &\times& (1-\eta) &\times& (1-\zeta) \\
N_1 &=& \xi &\times& (1-\eta) &\times& (1-\zeta) \\
N_2 &=& \xi &\times& \eta &\times& (1-\zeta) \\
N_3 &=& (1-\xi) &\times& \eta &\times& (1-\zeta) \\
N_4 &=& \zeta \\
\end{array}
PRISM: Linear Prism/Wedge
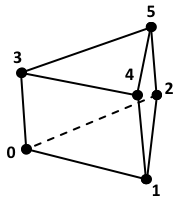
\begin{array}{r c l c l c l}
N_0 &=& (1-\xi) - \eta &\times& (1-\zeta) \\
N_1 &=& \xi &\times& (1-\zeta) \\
N_2 &=& \eta &\times& (1-\zeta) \\
N_3 &=& (1-\xi) - \eta &\times& \zeta \\
N_4 &=& \xi &\times& \zeta \\
N_5 &=& \eta &\times& \zeta \\
\end{array}
Add a New Lagrange Element
Warning
This section is under construction.
Isoparametric Mapping
Warning
This section is under construction.
Quadratures
Warning
Support for Quadratures in Mint is under development.
Add a New Finite Element Basis
Warning
This section is under construction.






