UniformGrid¶
The UniformGrid is inspired by and can be used to implement the
Cell list.
This data structure tiles a rectilinear region of interest into
non-intersecting subregions (or “bins”) of uniform size. Each bin gets a
reference to every object in the region of interest that intersects that bin.
UniformGrid can be used when a code compares each primitive
in a collection to every other spatially-close primitive, such as when
checking if a triangle mesh intersects itself. The following naive
implementation is straightforward but runs in \(O(n^2)\) time, where
\(n\) is the number of triangles.
void findTriIntersectionsNaively(std::vector<TriangleType>& tris,
std::vector<std::pair<int, int>>& clashes)
{
int tcount = static_cast<int>(tris.size());
for(int i = 0; i < tcount; ++i)
{
TriangleType& t1 = tris[i];
for(int j = i + 1; j < tcount; ++j)
{
TriangleType& t2 = tris[j];
if(intersect(t1, t2))
{
clashes.push_back(std::make_pair(i, j));
}
}
}
}
We want to call intersect() only for triangles that can intersect, ignoring
widely-separated triangles. The UniformGrid enables this optimization. In
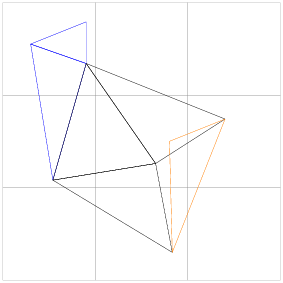
the following figure, the UniformGrid divides the region of interest into
three by three bins outlined in grey. A triangle \(t\) (shown in orange)
will be compared with neighbor triangles (shown in black) that fall into the
bins occupied by \(t\). Other triangles (shown in blue) are too far away
to intersect and are not compared with \(t\).
First, construct the UniformGrid and load it with triangles.
#include "axom/spin/UniformGrid.hpp"
// the UniformGrid will store ints ("thing" indexes) in 3D
using UniformGridType = axom::spin::UniformGrid<int, in3D>;
BoundingBoxType findBbox(std::vector<TriangleType>& tris);
BoundingBoxType findBbox(TriangleType& tri);
UniformGridType* buildUniformGrid(std::vector<TriangleType>& tris)
{
// Prepare to construct the UniformGrid.
BoundingBoxType allbbox = findBbox(tris);
const PointType& minBBPt = allbbox.getMin();
const PointType& maxBBPt = allbbox.getMax();
int tcount = static_cast<int>(tris.size());
// The number of bins along one side of the UniformGrid.
// This is a heuristic.
int res = (int)(1 + std::pow(tcount, 1 / 3.));
int ress[3] = {res, res, res};
// Construct the UniformGrid with minimum point, maximum point,
// and number of bins along each side. Then insert the triangles.
UniformGridType* ugrid =
new UniformGridType(minBBPt.data(), maxBBPt.data(), ress);
for(int i = 0; i < tcount; ++i)
{
TriangleType& t1 = tris[i];
BoundingBoxType bbox = findBbox(t1);
ugrid->insert(bbox, i);
}
return ugrid;
}
Then, for every triangle, look up its possible neighbors
void findNeighborCandidates(TriangleType& t1,
int i,
UniformGridType* ugrid,
std::vector<int>& neighbors)
{
BoundingBoxType bbox = findBbox(t1);
// Get all the bins t1 occupies
const std::vector<int> bToCheck = ugrid->getBinsForBbox(bbox);
size_t checkcount = bToCheck.size();
// Load all the triangles in these bins whose indices are
// greater than i into a vector.
for(size_t curb = 0; curb < checkcount; ++curb)
{
std::vector<int> ntlist = ugrid->getBinContents(bToCheck[curb]);
for(size_t j = 0; j < ntlist.size(); ++j)
{
if(ntlist[j] > i)
{
neighbors.push_back(ntlist[j]);
}
}
}
// Sort the neighboring triangles, and throw out duplicates.
// This is not strictly necessary but saves some calls to intersect().
std::sort(neighbors.begin(), neighbors.end());
std::vector<int>::iterator jend =
std::unique(neighbors.begin(), neighbors.end());
neighbors.erase(jend, neighbors.end());
}
and test the triangle against those neighbors.
void findTriIntersectionsAccel(std::vector<TriangleType>& tris,
UniformGridType* ugrid,
std::vector<std::pair<int, int>>& clashes)
{
int tcount = static_cast<int>(tris.size());
// For each triangle t1,
for(int i = 0; i < tcount; ++i)
{
TriangleType& t1 = tris[i];
std::vector<int> neighbors;
findNeighborCandidates(t1, i, ugrid, neighbors);
// Test for intersection between t1 and each of its neighbors.
int ncount = static_cast<int>(neighbors.size());
for(int n = 0; n < ncount; ++n)
{
int j = neighbors[n];
TriangleType& t2 = tris[j];
if(axom::primal::intersect(t1, t2))
{
clashes.push_back(std::make_pair(i, j));
}
}
}
}
The UniformGrid has its best effect when objects are roughly the same size and
evenly distributed over the region of interest, and when bins are close to the
characteristic size of objects in the region of interest.